Homework
assignments and solutions will be posted here
You are encouraged to work with your peers on your homework but everyone needs to turn in original work for the solution. The goal of these assignments is for you to practice solving CM program so that you will be confident and competent in doing them in the final exam and the qualifying exams later on. Since CM is one of the standard graduate physics courses, there are accessible solutions for most problems out there. You can use them as reference but I would strongly suggest you to attempt these problems without relying on them in your initial attempts.
Late homework policy: Homework loses 30% of
its value
each day after the due date.
Homework #12
Please note that we will most likely be covering materials on rigid body motions up until the last lecture. Read ahead and use the extra time in-between homeworks to review older materials.
Due: Practice only
- Goldstein, 3rd edition, Chapter 5, problems 9, 15, 17 (see below), 26
- Marion and Thronton, 5th edition, Chapter 11, problem 2 (note: do this problem before Goldstein 5.17.)
- Extra Problem: See below
Comments:
- Problem 5.9: After you have written out the Euler's equation correctly with all quantities (w and N) in their proper body axes coordinates, it is just a lot of algebra to manipulate the three equations into the desired two constants of motion. The goal is to write the equations in such a way that the LHS corresponds to a full time derivative of an experession and the RHS is zero.
- Problem 5.15: The integration is simplier if one calculates the moments of inertia with the axis of rotation located at the tip of the triangle first. Then, use the parallel axis theorem to move the axis of rotation to the CM. To be concrete, take the size of the triagle to be (a, a, sqrt(2)a). Calculate the total mass M of the triangle and express your answer in terms of M and a.
- Problem 11.2 and 5.17: Again, calculate the total mass M of the cone and express your moments of inertia in terms of M, R, h, and a.
Text for MT 11.2: Calculate the moments of inertia I1, I2, I3 for a homogeneous cone of mass M whose height is h and whose base has a radius R. Choose x3-axis along the axis of symmetry of the cone. Choose the origin at the apex of the cone, and calculate the elements of the inertia tensor. Then make a transformation such that the center of mass of the cone becomes the origin, and find the principal moments of inertia.
- Problem 5.26: Express your answers in terms of the precession speed W, initial conditions (f0, q0, y0)) and the principle moments of inertia (I1, I2, I3) for the symmetric body.
- Extra Problem: Let I1, I2, I3 be the three principal moments of inertia relative to the center of mass of a rigid body and suppose that all these moments are different and they are ranked according to I1> I2> I3. The rigid body is set to spin around one of its principle axes in free space (with no external force) with an angular velocity w. Show that the motion is stable if the object is spinning about the principal axes corresponding to I1 and I3 and unstable about the principal axis corresponding to I2. Explain this analytically using Euler's equations.
The solution is separated into the following pdf files:
Homework #11
Due: November 29, 2021
- Levi-Civita practice; use the Levi-Civita tensor to prove the following vector identities:
- Goldstein, 3rd edition, Chapter 4, problem 15
- Goldstein, 3rd edition, Chapter 4, problem 21, 24, 25
Comments:
- Problem 4.21: To fill in more details about the problem, assume that you are located in the northern hemisphere at a latitude of ao. You should also pick a local coordinate system which has its z-axis normal to ground. The simplest way to solve this problem is to assume the angular frequency of Earth's rotation to be small and you can solve the set of coupled ODEs perturbatively. Starting with the zero order solution (O(w0)), you can obtain the 1st order solution (O(w1)) by subsiting the 0th order solution back into the couple ODEs. You can also ignore the centrigugal force for this problem.
The solution is separated into the following pdf files:
Homework #10
Due: November 22, 2021 (If you need more time, you can turn in HW#10 on Wednesday or Thursady)
- Goldstein, 3rd edition, Chapter 6, problem 4
- Goldstein, 3rd edition, Chapter 6, problems 12
- additional problem: See below
Comments:
- Problem 6.4: For convenience, write your expression in terms of M=m1+m2 and ε =m2/M.
- Additional Problem:
A particle with mass m is constrained to move under gravity on a smooth surface give by the equation:
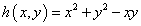 .
Also see picture of the situation here.
.
Also see picture of the situation here.

- Use the lagrangian formalism to find the equations of motion for the particle.
- Consider small oscillations about the orgin, what are the frequencies for teh normal modes?
- If one is to release the mass close to the origin, what must be the ratio between the x and y displacements so that only the higher frequency normal mode oscillation will be excited?
The solution is separated into the following pdf files:
Homework #9
Due: November 15, 2021
- Goldstein, 3rd edition, Chapter 9, problems 21, 24, 25
- additional problem #1: See below
- Goldstein, 3rd edition, Chapter 10, problem 5
Comments:
- Problem 9.21: To prove that the given quantity is a the constant of motion by directly calculating its Poisson bracket with H.
- Problem 9.25: First, try to see what transformation might be needed to get your transformed Hamiltonian in the right form. Then, try to show the required transformation is canonical. For simplicity, assume all physical parameters for the desired harmonic oscillator to be 1.
- additional problem #1: A particle of mass m described by one generalized coordinate q moves under the influence of a potential V(q) and a damping force
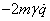 proportional to its velocity.
proportional to its velocity.
- Show that the following Lagrangian gives the desired equation of motion.
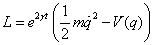
- Obtain the Hamiltonian H(q,p,t) for this system.
- Consider the following generating generating function:
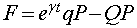
obtain the canonical transformation from (q,p) to (Q,P) and the transformed Hamiltonian K(Q,P,t).
- Pick
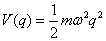 as a harmonic potential with a natural frequency
as a harmonic potential with a natural frequency 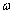 . Show that the transformed Hamiltonian yields a constant of motion.
. Show that the transformed Hamiltonian yields a constant of motion.
- Obtain the solution Q(t) for the damped oscillator in the under damped case
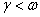 by solving Hamilton's equations in the transformed coordinates. Then, write down the solution q(t) using the canonical coordinates obtained in part (c).
by solving Hamilton's equations in the transformed coordinates. Then, write down the solution q(t) using the canonical coordinates obtained in part (c).
The solution is separated into the following pdf files:
Homework #8
Due: November 8, 2021
- Goldstein, 3rd edition, Chapter 8, problem 2, 7
- Marion and Thronton, 5th edition, Chapter 7, problems 29a,b, 30
link
- Goldstein, 3rd edition, Chapter 9, problem 2
Comments:
- Problem 8.2: You should note that under the gauge transformation, pj in the orginal hamiltonian function H(q,p,t) is no longer independent from the qj's.
- Problem 7.29: You only need to do parts a and b.
Consider the mass-on-a-spring pendulum described in problem Problem 7-15 (similar to Goldstein 1.24 in HW#3). The pendulum's point of support rises vertically with a constant acceleration a.
- Use the Lagrangian method to find the equations of motion.
- Determine the Hamiltonian and Hamilton's equations of motion.
- Problem 7.30: Consider any two continueous funcions of the generalized coordinates and momenta g(qk,pk) and h(qk,pk). The Poisson brackets are defined by
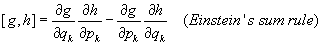
Vertify the following properties of the Poisson brackets: (where H is the Hamiltonian)
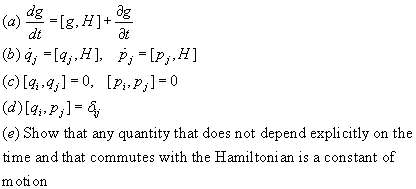
- Problem 9.2: You just need to show that the given transformation is canonical. We will derive the generating function in class.
The solution is separated into the following pdf files:
Homework #7
Due: October 25, 2021
- Goldstein, 3rd edition, Chapter 3, problem 18, 19b, 20b
- Goldstein, 3rd edition, Chapter 8, problem 1
- Marion and Thronton, 5th edition, Chapter 7, problems 28
Comments:
- Problem 3.18: This problem refers to the following result from Chapter 2, Problem 11 (Goldstein, 3rd ed.)
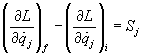 , where Sj is the generalized impulse force corresponding to qj.
, where Sj is the generalized impulse force corresponding to qj.
- Problem 3.19b and 3.20b: These two prolems are continuation from your previous assignment #6.
- Problem 3.19b: Note that there is a misprint here. The mathmatical expression for the answer should be:
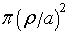 . Similar to our discussion in class, consider a small perturbation to the circular orbit, i.e. r = r0(1+x), where x is small. Subsitute this perturbation into Eq. 3.34, keeping only linear terms in x, and find the solution to the linearized differential equation for x. To get the final answer, you also need to assume that ρ/a << 1.
. Similar to our discussion in class, consider a small perturbation to the circular orbit, i.e. r = r0(1+x), where x is small. Subsitute this perturbation into Eq. 3.34, keeping only linear terms in x, and find the solution to the linearized differential equation for x. To get the final answer, you also need to assume that ρ/a << 1.
- Problem 8.1: Start with the Legerdre transform and the Hamilton's equations and derive the EL equations by assuming the functional dependence of both L and H on the stated independent variables.
The solution is separated into the following pdf files:
Homework #6
Due: October 18, 2021
- Goldstein, 3rd edition, Chapter 3, problem 13, 19a, 20a
- Marion and Thronton, 5th Edition, Chapter 8, problem 34 (see also Example 7-4 in M&T, 5th)
A particle of mass m is constrained to move on the inside surface of a smooth cone of half-angle alpha
a (see picture below).
The particle is subject to a gravitational force. Let the axis of the
cone be oriented vertically, and let this correspond to the z-axis. Let
the apex of the cone be located at the origin, and use the
corresponding cylindrical coordinates.
- Obtain the Lagrange equations of motion in two ways: (1) by
using proper generalized coordinates obtained by eliminating z via
the constraint equation, and (2) using the improper generalized
coordinates r, theta, and z, and introducing a Lagrange multipler.
- Reduce the problem to a one-dimensional problem. Show that the particle moves in an effective potential given by

(Note: If we are going to follow Goldstein's formalism in identifying the RHS of the 1D equation of motion (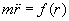 ) as the effective force, then there should be an overall sin2 a factor multiplied to the originally expression given in M&T.) ) as the effective force, then there should be an overall sin2 a factor multiplied to the originally expression given in M&T.)
- Graph (by hand!) the effective potential. Show that the turning points
of the motion can be found from the solution of a cubic equation in r.
Show further that only two of the roots are physically meaningful, so
that the motion is confined to lie within two horizontal planes that
cut the cone.
|
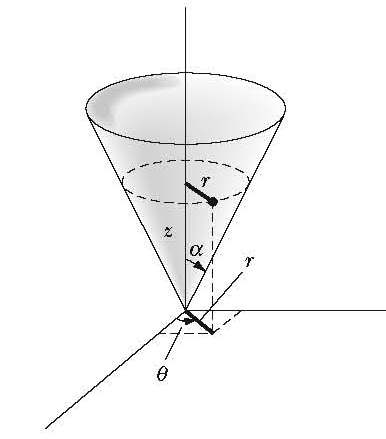
|
Comments:
- Problem 3.13:
For a power law potential in a central force, use Eq. 3.33 or 3.34 as the differential equation for the orbit. To visualize the situation, consider the following diagram for the orbit:
For a central force problem, angular momentum is a conserved quantity and is given by
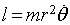 |
 |
- Problem 3.19: We will save part b until next time.
- Problem 3.20: We will save part b until next time.
The solution is separated into the following pdf files:
Homework #5
Due: October 12, 2021 (two weeks)
- Goldstein, 3rd edition, Chapter 2, problems 20, 21, 24
- Goldstein, 3rd edition, Chapter 1, problem 21
- Goldstein, 3rd edition, Chapter 3, problem 10, 11
Comments:
- Problem 2.20: For this problem, repeat the calculations for the equations of motion in both coordinate systems as suggested in the problem. The Cartestian coordinate system is easy to set up but you need to be careful in setting up the coordinate system for the mass m with y normal to the incline surface.
- Problem 2.21: Assume that both springs have the same k. That's what the text says, but in the figure there's a k and a K. So let k=K. For the two set of generalized coordinates, one can take the standard Cartestian (x,y) coordinates as the "laboratory" generalized coordinates and in the rotating frame, one can use (r, l) as the generalized coordinates where (r + r0) is the location of the carriage on the main rotating beam and l is the location of the mass m along the second ridig beam attached perpendicular to the main beam.
- Problem 2.24: Take the derivatives of the action I with respect to aj, then set them to zero.
- Problem 1.21: For this problem, solve for the equation of motion using the standard Lagrangian formalism that we have been doing. Then, to reduce the problem to an effective one dimensional problem and to interpret its physical significance, one can apply an effective potential analysis to the resulting set of differential equations similar to the central force problems in Goldstein (section 3.3).
- Problem 3.10: For the final answer, take the approximation that M >> mcomet and a << 1.
- The solution is separated into the following pdf files:
Homework #4
Due: September 27, 2021
- Goldstein, 3rd edition, Chapter 2, problems 12, 14, 16, 17, 18
Comments:
- Problem 12: Recall that in getting the regular Lagrange equations, we used
integration by parts. Here you do the same thing multiple times. Please
write neatly!!
- Problem 14: Be very careful writing down the equations of constraint. The
no-slipping condition is subtle. If in doubt, email me what you get and I'll confirm it if it's right.
- Problem 16: Please note that some version of the text has a typo for the point transform. The correct one for this problem should be s=exp(gamma*t/2)*q.
- Problem 17: Reduction to quadrature means that you should express the results
as an integral. So, if you could actually evaluate that integral (numerically or analytically, you'd
have the complete integration.
- Problem 18: For consideration of the stationary points, its velocity and acceleration should be zero.
- The solution is in two separate pdf files:
Homework #3
Due: September 20, 2021
- Goldstein, 3rd edition, Chapter 1, problems 20, 22, 23, 24 (a & b)
- Goldstein, 3rd edition, Chapter 2, problems 1, 4
Comments:
- Problem 20: If your book is the 5th printing or earlier of the 3rd edition, your Lagrangian might not be printed correctly. The correct Lagragian for this problem should be:

- Problem 24: You only need to do part a and b only for now. We will come back to the other parts later in the semester when we talked about oscillations and nonlinear dynsmics.
- Problem 2.1 and 2.4 involves two integrals which might require one or two math "tricks". If you get stuck, please ask me for hints
- The solution is in two separate pdf files:
Homework #2
Due: September 13, 2021
I am putting this set out now so that you all can take a look at them earlier.
- Goldstein, 3rd edition, Chapter 1, problems 8, 9, 10, 14, 15, 19
Comments:
- Problem 9: Make sure you check the errata web page. In my 5th printing,
there's the speed of light "c", which must be set equal to 1 to make the units match the
text.
- Problem 15: This is long, but straightforward problem. Save it as your last problem. Without loss of generality and to simplify unnecessary algebric complexity, I recommend choosing your
coordinate system so that
 coincides
with
coincides
with  , so that
, so that 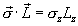 .
Alternatively, you can use this vector identity:
.
Alternatively, you can use this vector identity: 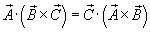 to express
to express 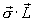 in a way that makes taking derivatives easy.
in a way that makes taking derivatives easy.
- Problem 19: A spherical pendulum is a pendulum that can move such that the
mass can be anywhere on the surface of a sphere. This is to be
distinguished from a plane pendulum, in which the mass can be anywhere
on a circle.
- The solution is in two separate pdf files:
Homework #1
Due: August 31, 2021
- Goldstein, 3rd edition, Chapter 1, problems (derivations) 1, 2, 3, 4, 7, and
- Additional Problem (Thornton and Marion 9.57):
- Show that a rocket in free space (i.e. no external force with initial velocity v0 and mass m0 attains a speed of v by ejecting mass (i.e. burning fuel), given by
v = v0 + u ln (m0/m),
where u is the exhaust velocity of the fuel and is assumed to be constant.
- If the rocket accelerates at a constant acceleration a to its final speed v, what is the total work done by the rocket engine?
- The solution is in two separate pdf files:
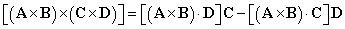
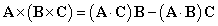
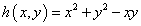 .
Also see picture of the situation here.
.
Also see picture of the situation here.

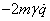 proportional to its velocity.
proportional to its velocity.
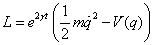
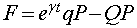
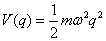 as a harmonic potential with a natural frequency
as a harmonic potential with a natural frequency 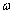 . Show that the transformed Hamiltonian yields a constant of motion.
. Show that the transformed Hamiltonian yields a constant of motion.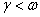 by solving Hamilton's equations in the transformed coordinates. Then, write down the solution q(t) using the canonical coordinates obtained in part (c).
by solving Hamilton's equations in the transformed coordinates. Then, write down the solution q(t) using the canonical coordinates obtained in part (c).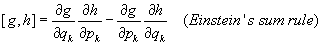
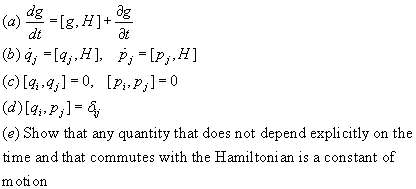
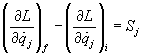 , where Sj is the generalized impulse force corresponding to qj.
, where Sj is the generalized impulse force corresponding to qj.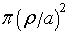 . Similar to our discussion in class, consider a small perturbation to the circular orbit, i.e. r = r0(1+x), where x is small. Subsitute this perturbation into Eq. 3.34, keeping only linear terms in x, and find the solution to the linearized differential equation for x. To get the final answer, you also need to assume that ρ/a << 1.
. Similar to our discussion in class, consider a small perturbation to the circular orbit, i.e. r = r0(1+x), where x is small. Subsitute this perturbation into Eq. 3.34, keeping only linear terms in x, and find the solution to the linearized differential equation for x. To get the final answer, you also need to assume that ρ/a << 1.
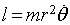


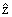 coincides
with
coincides
with 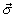 , so that
, so that 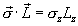 .
Alternatively, you can use this vector identity:
.
Alternatively, you can use this vector identity: 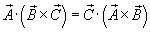 to express
to express 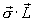 in a way that makes taking derivatives easy.
in a way that makes taking derivatives easy.