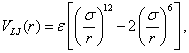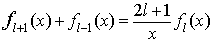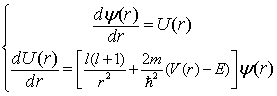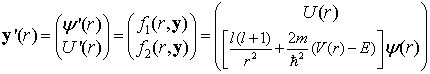SolutionRead through the description on quantum scattering in chapter 2 of Thijssen. This will help you to familiarize yourself with the problem. You should also consult your old quantum textbooks on the subject of partial wave expansions if you need more background materials.
For this problem, you need to calculate the total cross section for the Lennard-Jones potential:
where ε=5.9meV and σ=3.57A. [This potential has a minimum at r=σ.] In particular, you need to perform the following tasks:
- Write a RK4 code with fixed time steps to solve for the wavefunction given by the radial Schrodinger equation:
.
Follow the discussion on p. 22 for the consideration of the boundary condition at r=0. Since the potential blows up at r=0, your ode solver should integrate from a finite radial distance rmin away from zero. The phase shiftfor the scattered wave can then be extracted from the asymptotic wavefunction at a sufficient large r, rmax by a matching procedure described at the bottom of p. 18. For numerical simplicity, the factor
is chosen to be 6.12meV-1 σ -2 such that energy is measured in meV and length is measured in units of σ.
- As a test for your ode solver, you should plot the wavefunction for the following three cases:
The wavefunction away from the potential should look sinuoidal with a possible "delay" of its phase near the potential. Using the numerical values provided (see below), the amplitude of the wavefuntion (without normalization) should be on the order of roughly one. If your solution is exceedingly large or small, you most likely are doing something wrong.
- E = 1.0meV; l=0
- E = 0.5meV; l=4
- E = 1.4meV; l=5
- Calculate the total cross section for this scattering process for energy in the range [0.25,3.5] using:
,
where. For your numerical simulation, you can truncate your sum up to and including the l=6 term.
- Explain the physical meaning of the peaks observed in the total cross section graph.
Notes on Spherical Bessel functions:
To extract the phase shift from the potential, one matches the wavefunction solution to its asymptotic form (Eq. 2.4 in Thijssen) at two different r values larger than rmax. This matching procedure requires one to evaluate the Spherical Bessel functions jl(kr) (first kind) and nl(kr) (second kind) numerically. Similar to other special functions, the Spherical Bessel functions can be calculated using its recursion relation:
As in the case for the regular Bessel functions, the same recursion relation applies to both kinds of the Spherical Bessel functions so that it will be stable for nl(kr) and unstable for jl(kr).For the stable case (nl(kr)), one can directly evaluate the higher order ones using the recursion relation with the following initial conditions:
.
For the unstable case (jl(kr)), one can utilize the Miller's algorithm with the normalization condition:
.
For accurate results, you should start your backward iterations from l larger than 30.A summary of numerical values used for this problem:
e 5.9meV l up to and including l=6 rmin 0.5σ rmax 5σ h (RK4 stepsize) at least 1e-3 lmax for Miller's algorithm larger than 30
Although there are many pieces to this assignment, they are quite straight forward with different skills that you have learned from this semester. The radial Schrodinger equation is a second order differential equation and we can write it into a two dimensional first order ODE as follows:
In this case, the 1D RK4 algorithm can be extended by treating y(r)=(ψ(r),U(r)) as a two components vector and the above equation as a vector equation
The equations for the RK4 algorithm will be the same as in the one dimensional case except that we need to treat the relevant variables in those equation as a two components vector.A C implementation of this solution is given here . The wavefuntion for the three different cases are given below:
Fig. 1:(E=0.5,l=4)
Fig. 2:(E=1.0,l=0)
Fig. 3:(E=1.4,l=5)
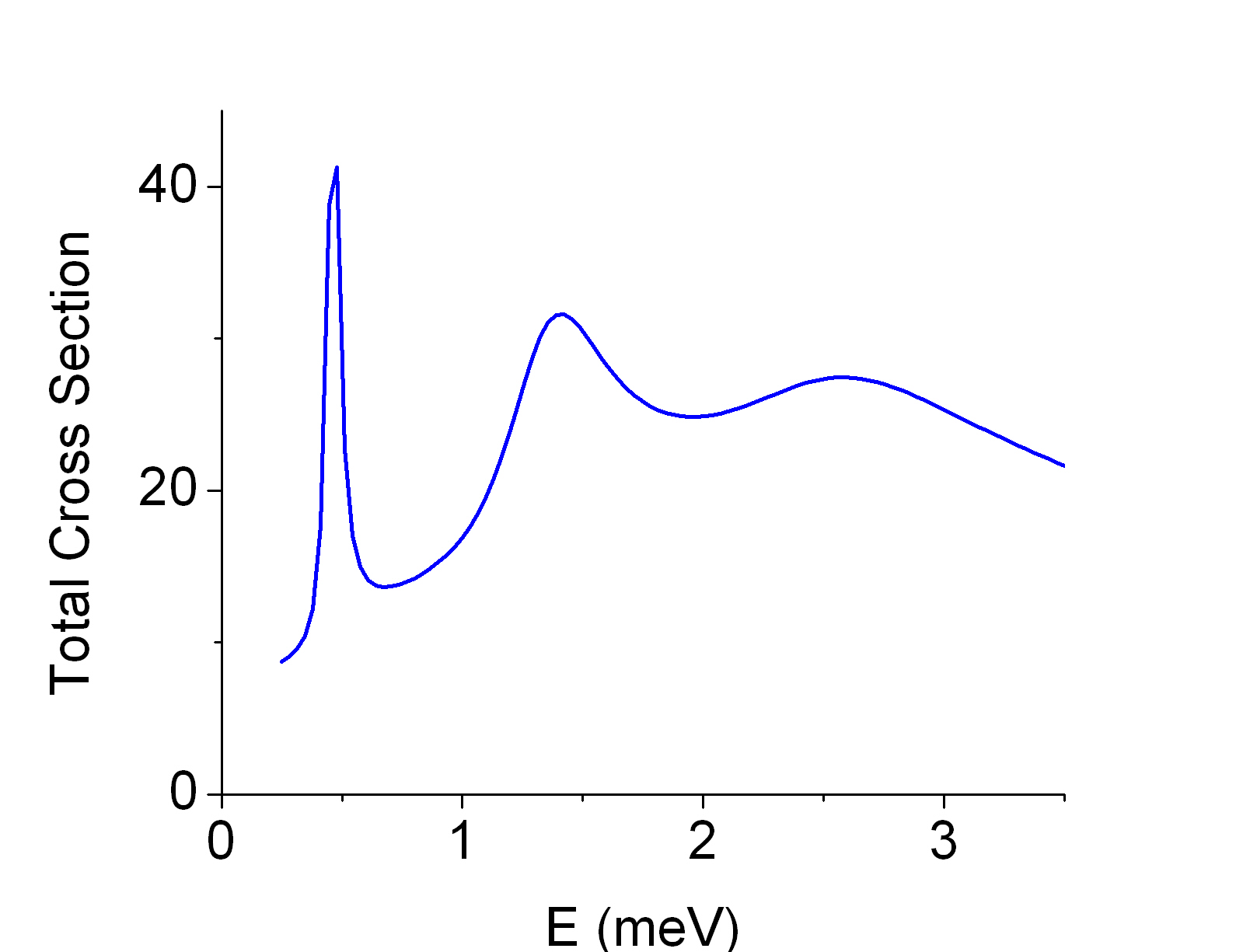
and the total cross section is given here:
Fig. 4.Total Cross Section vs. E
There are three prominent peaks visible in the cross section plot at E ~ 0.5, 1.4, and 2.6. These energies are near the scattering resonance energies of the potential. In particular, at E~0.5, the l=4 wave is in resonance with the potential; at E~1.4, l=5 wave is in resonance and finally at E~2.6, l=6 wave is in resonance. Near resonances, the wavefunction is temporary "trapped" by the potential so that the total cross section is maximal and the corresponding wave is scattered the most at those energies . One can see from the wavefunctions themselves that the waves are temporary "delayed" by the potential near resonances (Figs. 1 and 3).
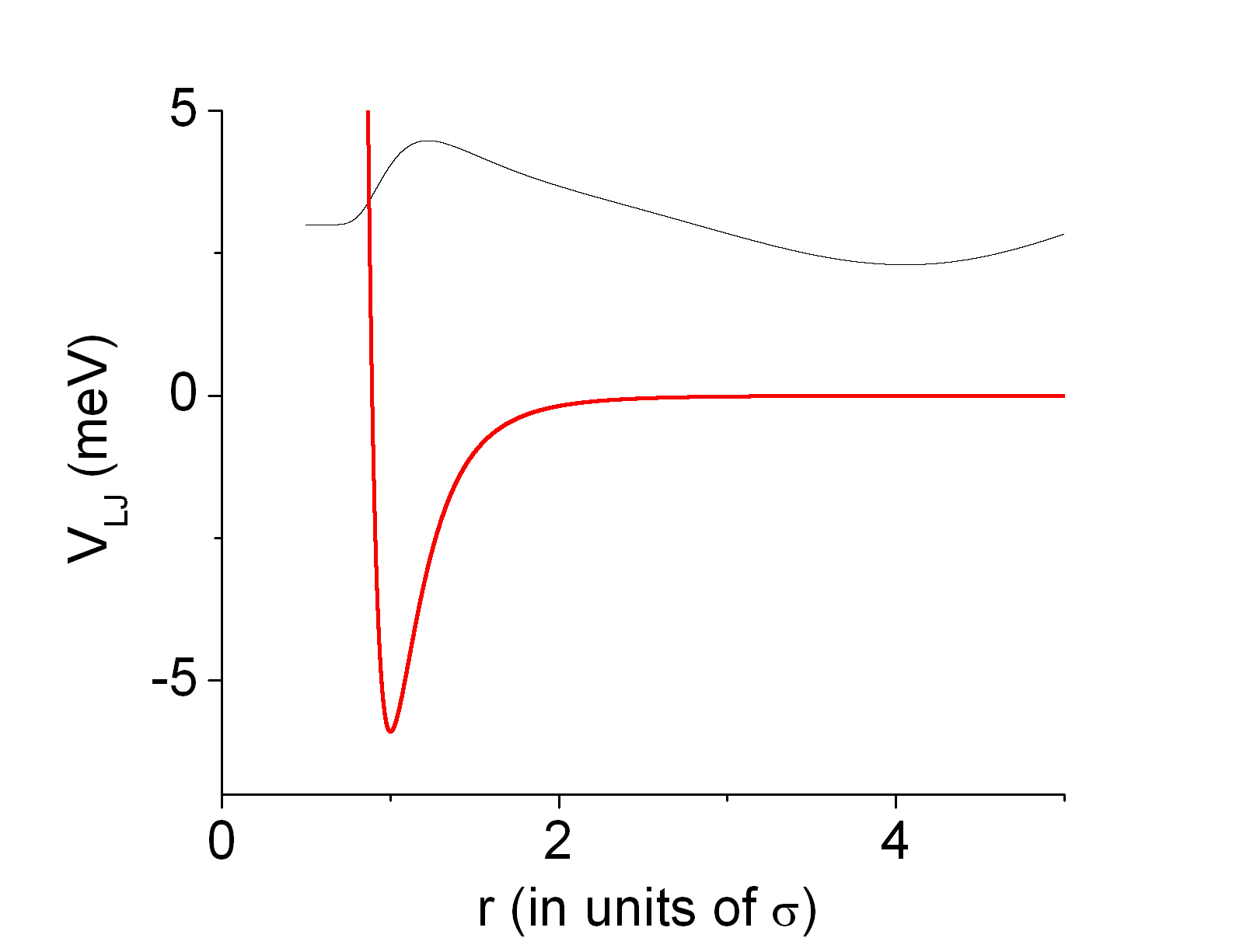
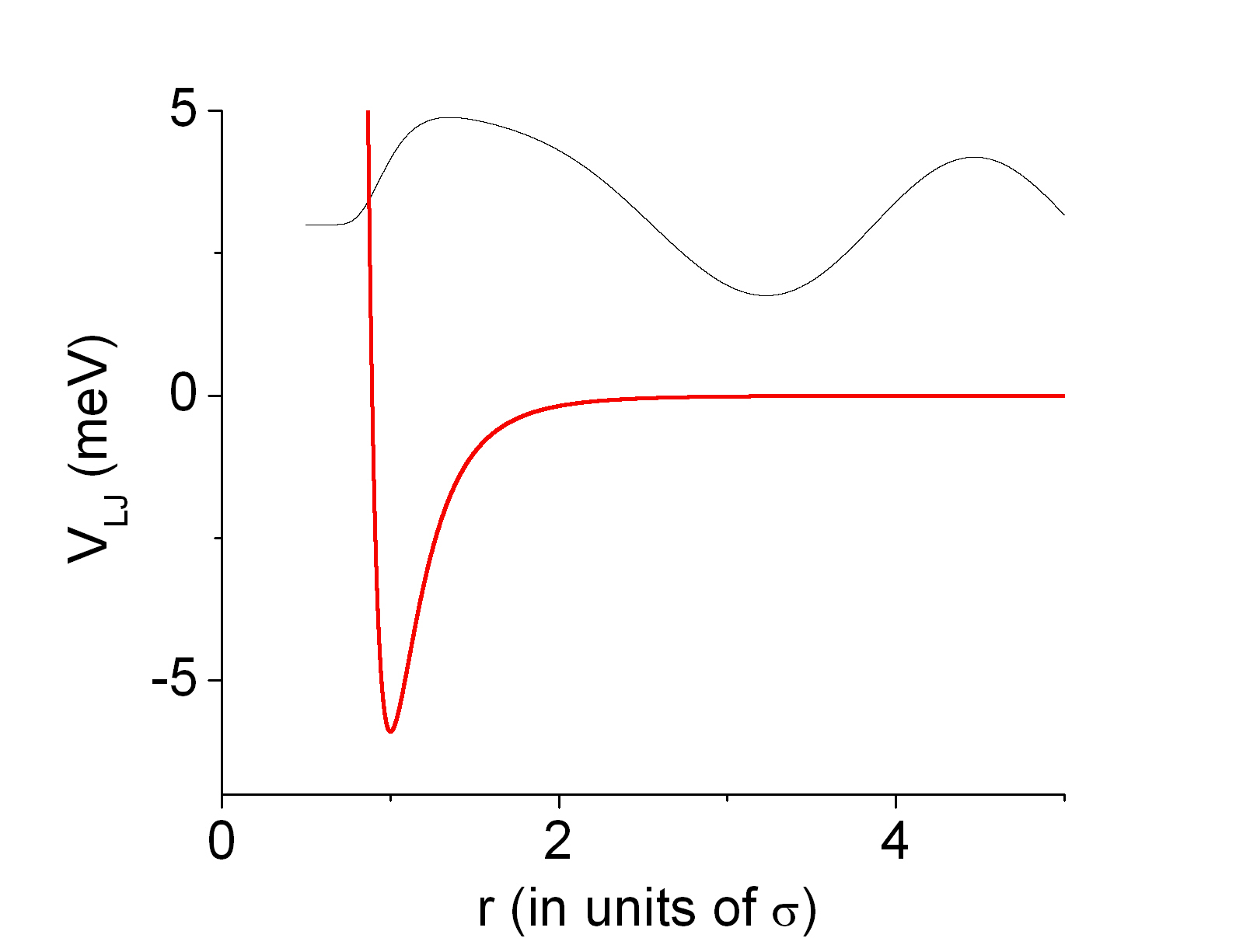
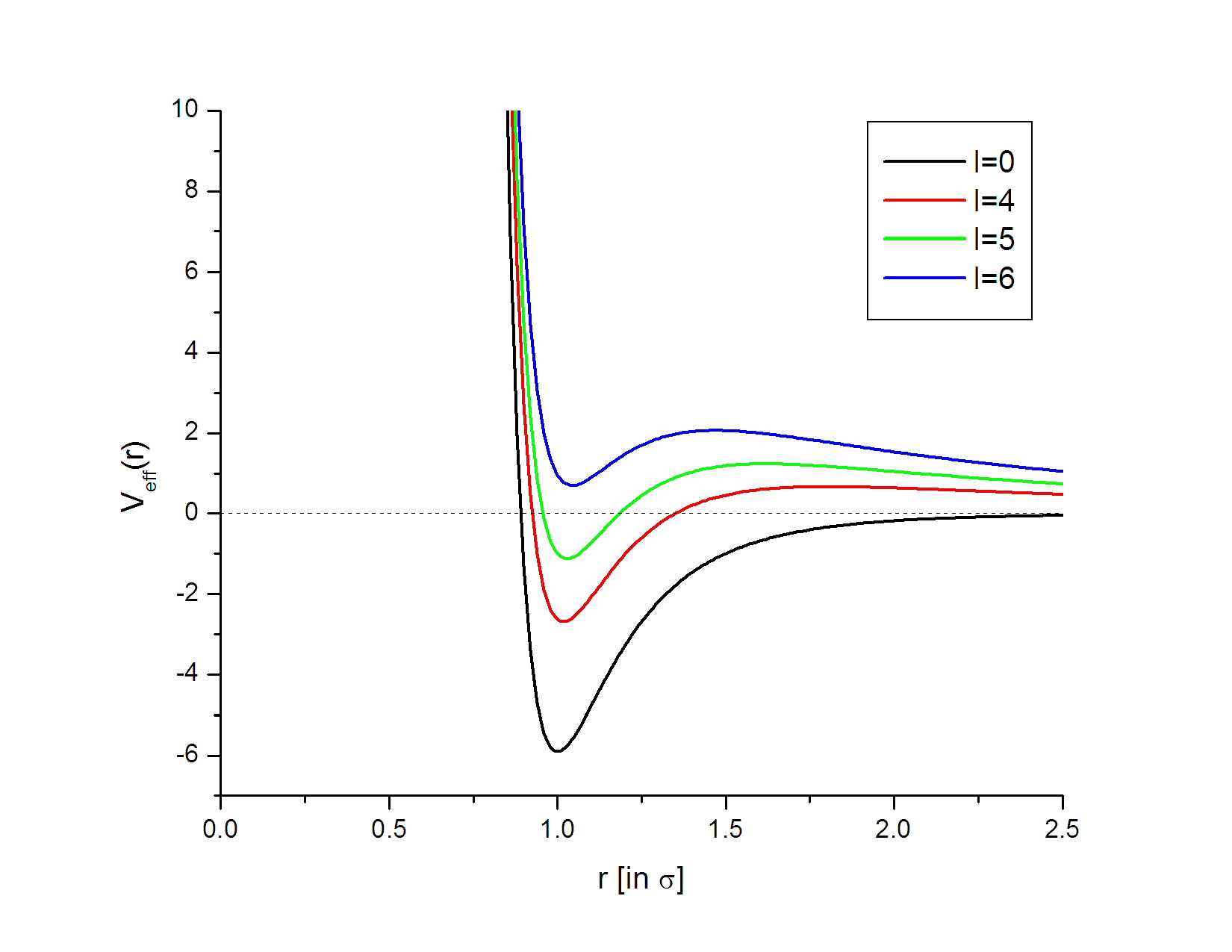
From the total cross section graph, one can also see that the resonance peaks are progressively sharper for partial waves with lower angular momentum (l value). This can also be heuristically understood in terms of the effective potential that the scattering wave is intereacting with. Here is a graph of the effective potential Veff
Fig. 5: Veff vs. r (in units of σ) for l=0,4,5,6
From this graph, one can see that the effective potential gets shallower as angular momentum quantum number increases so that the scattering wave "feels" less trapped by the potential and thus results in a less sharp (strong) resonance peak.
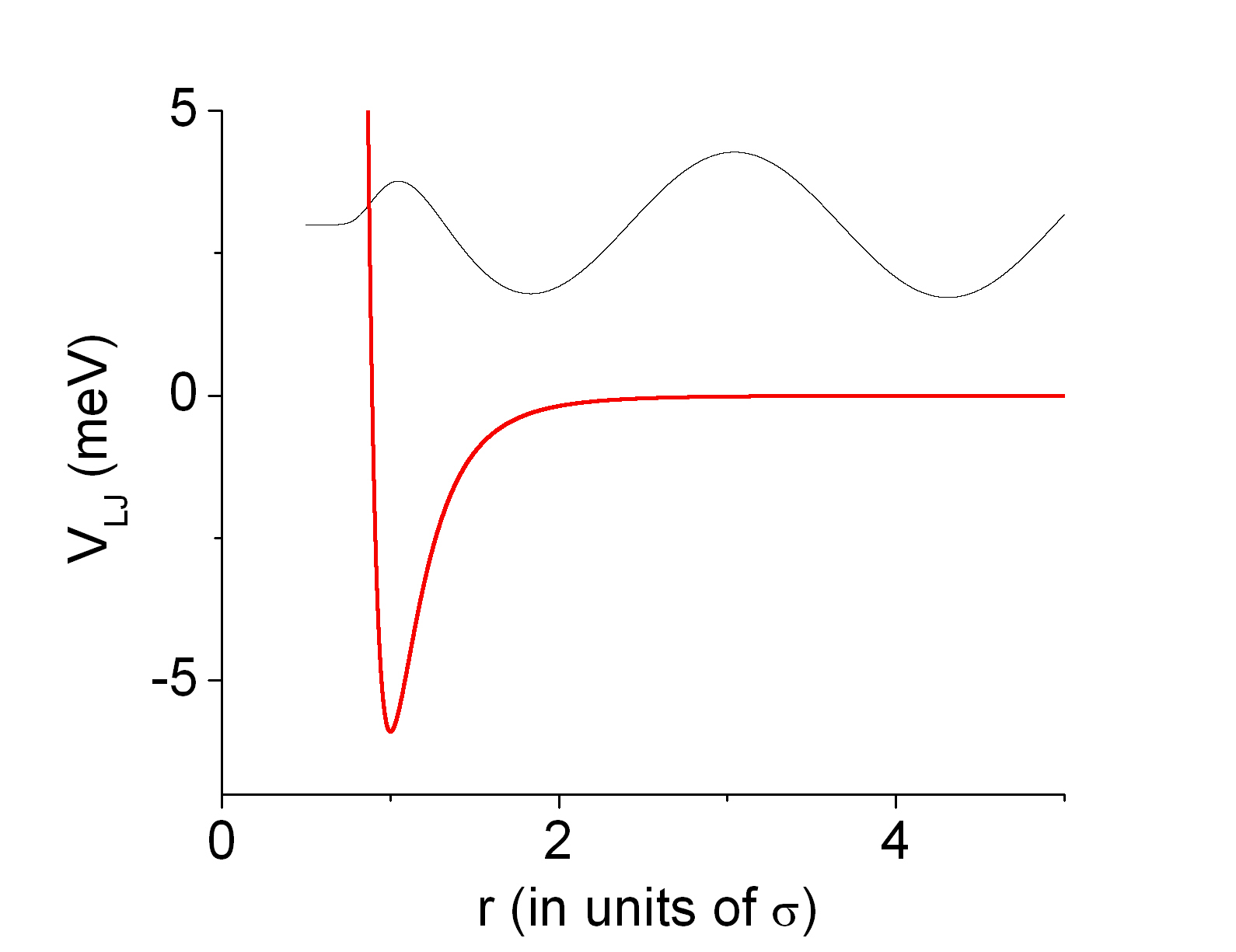
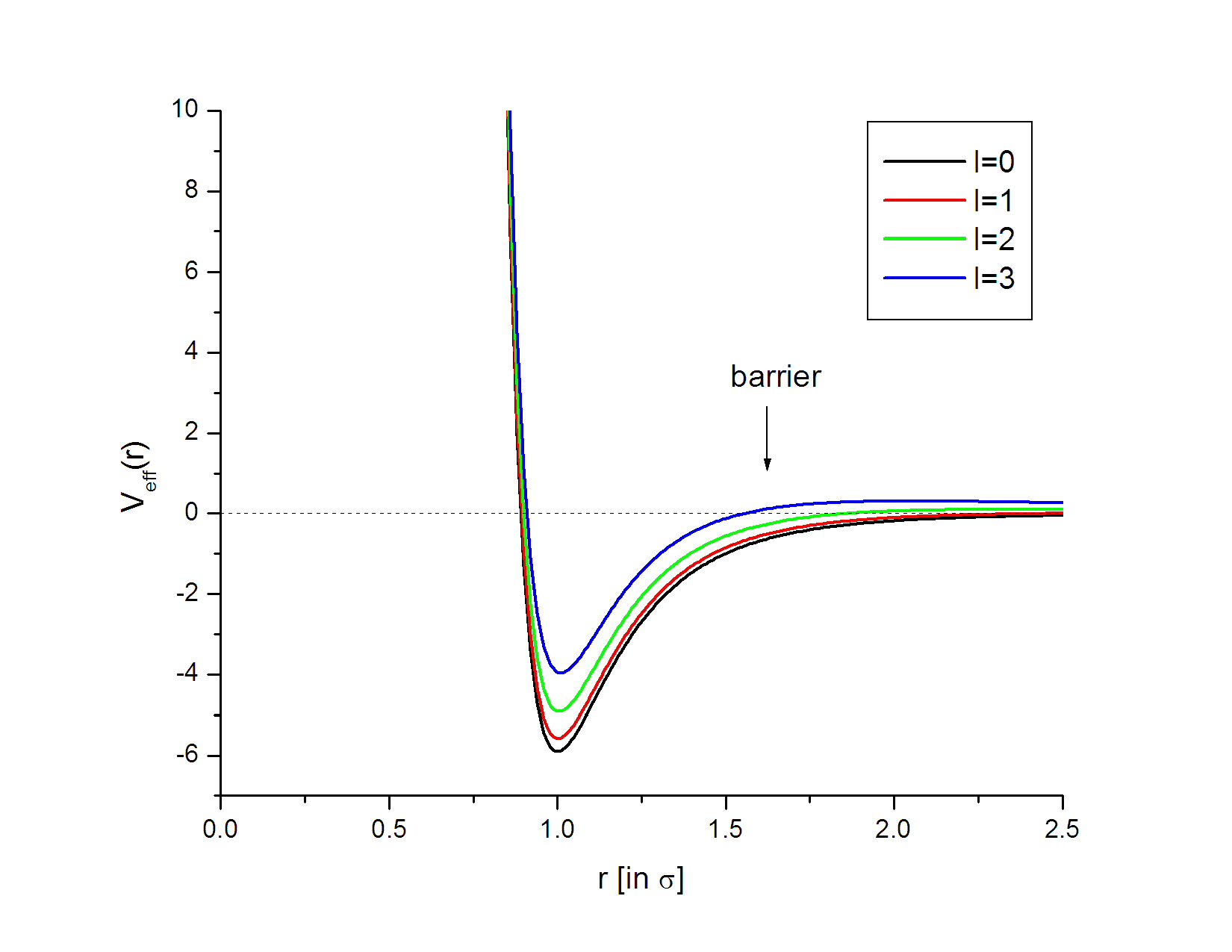
On the other hand, if one examines the effective potentail graphs for l=1,2,3 (see below), one can see that the barrier for "escaping" (through tunnelling) is relatively lower as compare to the previous case (l=4,5,6). As a result, the scattering wave (with positive E) with these lower angular momenta will be less likely to be temporary trapped by the potential and we do not expect to observe strong resonance peaks for these partial waves. Furthermore, those resonance energies will be very close to E~+0 (nearly bounded) and these values were not probed in this numerical experiment.
Fig. 6: Veff vs. r (in units of σ) for l=0,1,2,3