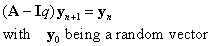Consider a string fixed at both end [0,L] and under uniform tension T. The amplitude u(x,t) of this vibrating string can be described by the following wave equation
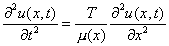
where μ(x) is the mass of the string per unit length. A stationary solution can be obtained by assuming a harmonic time dependence for the general solution
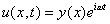
Then, by substituting this into the wave equation, we can lead to the following ordinary differential equation
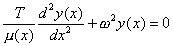
This is a boundary value problem with y(0)=y(L)=0. For μ(x) being a function of x, one way to solve this equation is by finite differences. Replacing the derivative in the above equation by its finite difference approximation, we have the difference equations
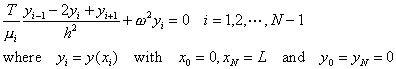
This set of difference equations can be written as a matrix equation given below
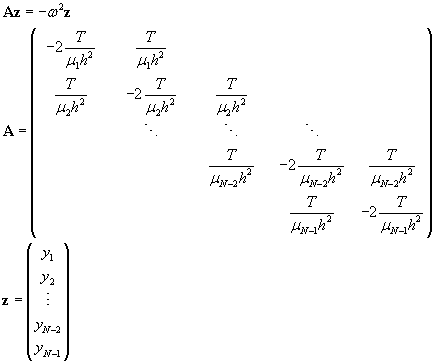
This is an eigenvalue equation and we can solve for the eigenfrequencies ω and the eigenmodes (standing waves) by the techniques which we have discussed in class. Note that the matrix equation obtained from finite difference consideration usually results in a tridiagonal form.
Take T=1000 Newtons, L=1 m, and 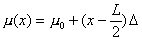 with μ0=0.954 g/m (average mass density) and Δ=0.5 g/m2 (mass density variations per unit length).
with μ0=0.954 g/m (average mass density) and Δ=0.5 g/m2 (mass density variations per unit length).
For this problem, perform the following task:
- Take h=0.05 m as your discretization size, use the matrix form of the finite difference equation to solve for the three lowest eigenfrequencies by finding the lowest three zeros of the characteristic equation det|A-Iλ|=0.
- With the same h as in part 1, solve for all the eigenvalues of A using the QR decomposition method. Compare your answers from part 1 and 2. (You are allowed to use NR for help on the QR eigenvalue solver.)
- For the lowest three modes, plot the eigenfunctions as a function of xi. These are discretized approximations of the standing waves. Since A is not a symmetric matrix, you can't get the eigenvectors directly from the QR decomposition method. On the other hand, since you have evaluated the eigenvalues already, eigenvectors can be computed using the inverse power iteration method.
Note:
- Since the mass density μ(x) is a function of x, A is NOT a symmetric matrix.
- The characteristic equation (a N-order polynomial) and its derivative for the tridiagonal matrix A can be evaluated efficiently by the following iterative scheme:

I have absorbed the minus sign on the right hand side of the matrix equation into the matrix A itself so that all eigenvalues are referring to the matrix
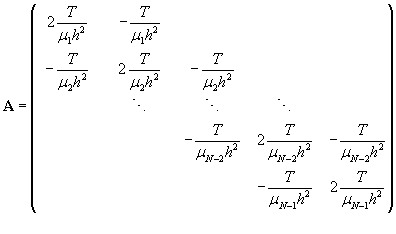
For part 1 of this problem, the eigenvalues are calculated using the direct method by finding the zero of the characteristic equation
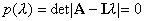 .
.
In this implementation, since both the characteristic equation and its derivative can be easily calculated using the following recursion relations,

the zero-finding method of choice is the Newton's Method.
One point which you need to play attention to is to get good initial guess for the location of the zeros. The best way is to make a rough plot of the function pN(λ). This is shown below
The algorithm starts with leftmost value in the graph before any zero crossings and moves forward to look for whenpn(λ) changes sign. Then it will return the right point after crossing zero as seed for the Newton's method. The increment steps are estimated from the graph of pn(λ).
The 19 zeros found with this method is given below in the following text file: eigval.dat.
The second part of the problem asks to find the eigenvalues of A by using the repeated QR transform method. In the special case when A is symmetric, the repeated application of the QR transform can reduced A to a diagonal metrix with eigenvalues given along the diagonal and their eigenvectors given by the sequence of Q's matrices. However, the matrix A from our nonuniform string is not symmetric and the best which we can expect from the repeated application of the QR transformation is to reduce A to a triangular matrix. In this case, the eigenvalues can still be easily read off from the diagonal elements if all eigenvalues are real. [For complex eigenvalues, the conjugate pairs will be determined by 2X2 Jordan subblocks along the diagonal.] For our problem with the nonuniform string, we expect all our eigenvalues to be real (as indicated by the solution in part 1). Algorithms for eigenvalue evaluation in the QR class are highly specialized and I don't mind that you use the ones provided by NR. Since our matrix is nonsymmetric, the appropriate routines from NR for use is "hqr". The eigenvalues obtain with this method is given in eigval.dat. Please note that the actual eigenfrequencies are given by sqrt(T λ/h2). [If you use Mathematica, the following link is a simple implementation of the most basic eigenvalue solver using QR decomposition without shifting and deflating the matrix. It takes roughly 100 iterations for the lower diagonal elements to reduce to less than 10-7. Eigenvalues can then be read off from the diagonal. Note that the "hqr" routine (with a proper shifting and deflation) in NR takes much less number of iterations to achive the same goal. Matlab's implementation will be similar.]
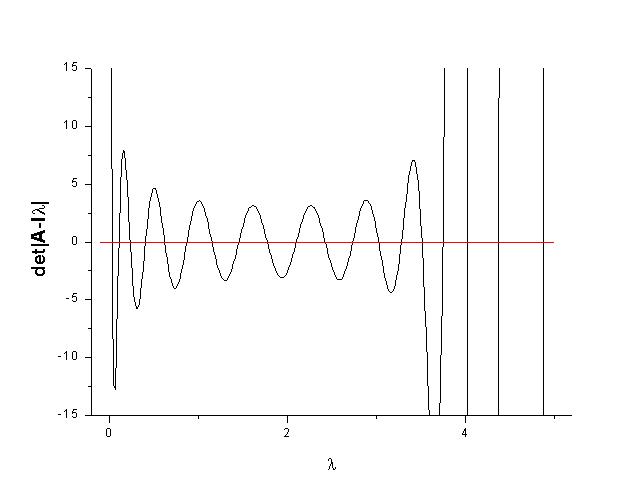
Since A is not symmetric, the eigenvectors cannot be directly obtained from the QR method above. They can to be calculated using an inverse power iteration method using the eigenvalues calculated from part 1 or 2. The inverse power iteration starts with a random unit vector y0. Then the repeated iteration of it using (A-Iq)-1 (with q~λi being a close estimate of the ture eigenvalue) should align it along the eigenvector corresponding to λi. The convergence is fast if q is close to the true eigenvalue since the covergence rate is determined by 1/(λi-q). However, numerically, one needs to play attention to the fact that the matrix (A-Iq) will also be nearly singular so that the evaluation of (A-Iq)-1 might be suspectible to round off errors. One method to take this into account is the solve for yn+1 using the following matrix equation without explicitly calculating (A-Iq)-1 and the matrix equation should be solved by a LU decomposition scheme with pivoting.
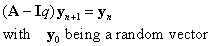
Note that a SVD solver should not be used in this case since the eigenvector corresponding to the eigenvalue λi-q is actually in the null space of (A-Iq) and a least square solution to (A-Iq)x=yn will not be appropriate.
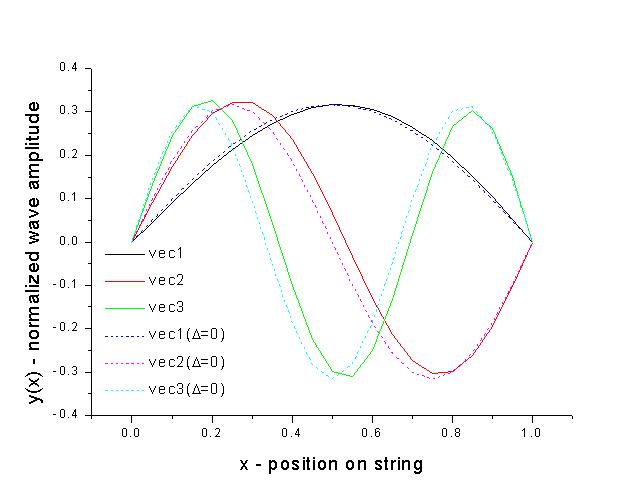
Here is a plot of the first five eigenvectors corresponding to the five modes with the lowest energies:
The qualitative features of these modes are as expected for a string clamped on its ends. As a comparision, I have also calculated the eigenvalues and eigenvectors for the case when the string is with an uniform density, i.e. Δ=0. The eigenvalues are given here and a comparision of the standing waves are given in the following graph,
A C implementation for the three parts of this program can be found here (qrstring.c). Its other dependent routines can be found here:
numcip.c - mainly vector and matrix allocations
numcip.h
random.c - random number generators
random.h
malgbr.c - linear algebra stuff
malgbr.h
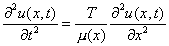
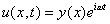
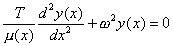
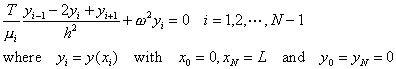
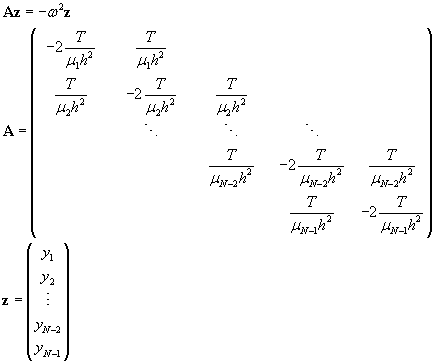
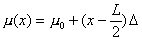 with μ0=0.954 g/m (average mass density) and Δ=0.5 g/m2 (mass density variations per unit length).
with μ0=0.954 g/m (average mass density) and Δ=0.5 g/m2 (mass density variations per unit length).

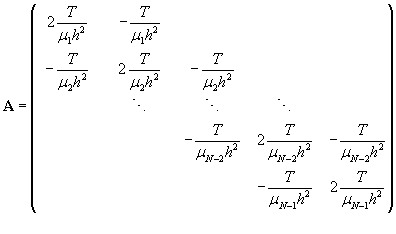
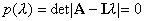 .
.