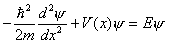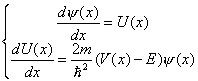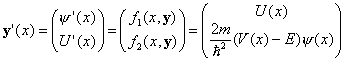Do the following for this problem:Solution
- Read through the description of the anharmonic oscillator problem in De Vires from p. 236 to p. 241. I will make some copies of the relevant pages for the class. This will help you to familiarize yourself with the problem. (Note: There is an error on page 236. Eq. 5.68 should read
- Write a code to implement the Runge-Kuta-Fehlberg algorithm with adaptative step sizes to solve for the wavefunction given by the 1D Schrodinger equation.
- With the anharmonic potential given by V(x)=0.5x2+0.25x4, find the lowest three eigenenergies- two even and one odd. Your answers should be accurate to single precision. (Note: here you need to combine the RKF-ODE solver with a zero-finding scheme.)
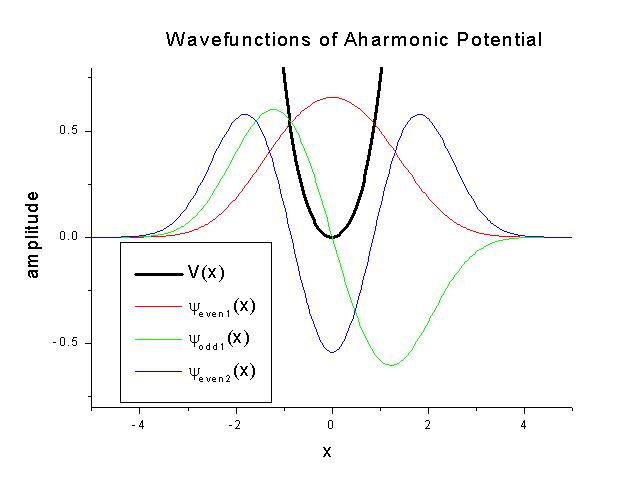
- Plot the normalized wavefunctions from x=-5A to x=5A for these three lowest eigenenergies. (Note: you will need to use your numerical integrator to find the normalization constant.)
Although this problem is relatively straight forward, it involves combining different numerical algorithms (ODE solvers, zero finding schemes, and numerical integrators) which you have learned this semester. The Schrodinger equation is a second order differential equation and we can write it into a two dimensional first order ODE as follows:
In this case, the Runge-Kutta-Fehlberg algorithm can be extended by treating y(x)=(ψ(x),U(x)) as a two components vector and the above equation as a vector equation (see pp. 226-227)
The equations (5.41-5.50) for the Runge-Kutta_Fehlberg algorithm on pp. 220-221 will be the same as in the one dimensional case except that we need to treat y in those equation as a two components vector.As described in the book, either the eigenfunction (even) or the derivative of the eigenfunction (odd) for this symmetric Hamitonian will vanish at x=0. Thus, the search for eigenenergies requires the search for zeros of the logarithmic derivative of the wavefunction at x=0. (For odd states, we need to search for zero for the inverse of the logarithmic derivative instead.) With a given test energy, the RKF-ODE solver is needed to propagate the wavefunction from a negative x value (here, we start x at -5A) to the middle of the potential well (x=0). A bisection algorithm is used to find the correct energy which will give you the zeros of corresponding criterion. Similar to our previous assignment, the success of the bisection method requires us to initially bracket the zero. This can be easily done by starting at some small energy E=0.1 and evaluate its RKF solved logarithmic derivative at x=0. We need to increment E so that the logarithm derivative changes sign. Then, we can start the bisection process. Since we are interested in the logarithmic derivative at x=0, we need to adjust the RKF-ODE solver so that it will end exactly at x=0.
There are two places where we need to compare our error with given tolerance levels. First, we need to ensure that the ODE solver is accurate to within a given tol by adjusting our step size h at each iterations (see the discussion in the book on adaptive step size and read thru their psudocodes for this part.). If the current one-step error |yRK4-yRK5| is larger than the maximum acceptable error |h|ε, the current step will not be used and a new one-step solution will be recalculated using a new smaller step size calculated using Eq. 5.50. For this problem, we set this tolerance level ε to be at 1e-9. Second, the bisection algorithm has a tolerance level for the termination of the bisection process. In this case, we are interested in the vanishing of the logarithmic derivative of the wave function at x=0 and we have taken this tolerance level to be at 1e-9. This is chosen to be comparable to the tolerance level for the RKF-ODE solver. (Note that since the arbitrary scaling factor for the wavefunction has been taken out of the ratio between ψ' and ψ, this tolerance corresponds to an absolute instead of a relative error.)
A C implementation of this solution is given here and the three lowest eigenenergies are found to be:
- 1st Even: 2.04746294
- 1st Odd: 6.90334876
- 2nd Even: 12.9547073
The wavefunctions should be normalized by requiring the integral of ψ*ψ over the entire range to be 1. (Since the potential is symmetric, we only need to integrate ψ*ψ on half of the x-axis and requiring the result to be 1/2.) The numerical integration scheme (a simple trapezoid rule) is used as a part of the combined program. The following are the calculated normalized wavefunctions.