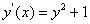Write a computer code to solve the differential equationSolutions
for x in the range of [0,1] using Euler's method, modified Euler's method, and improved Euler's method, with the initial condition y(0)=0. Plot your results for step size h=0.05, 0.10, 0.15, and 0.20, along with the exact result. Compare and discuss the three methods.
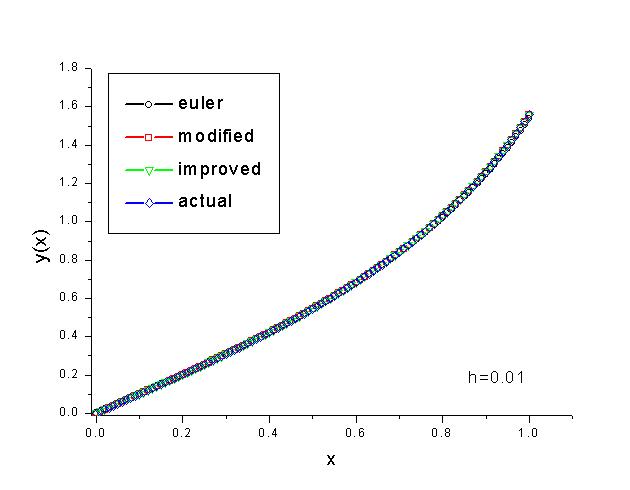
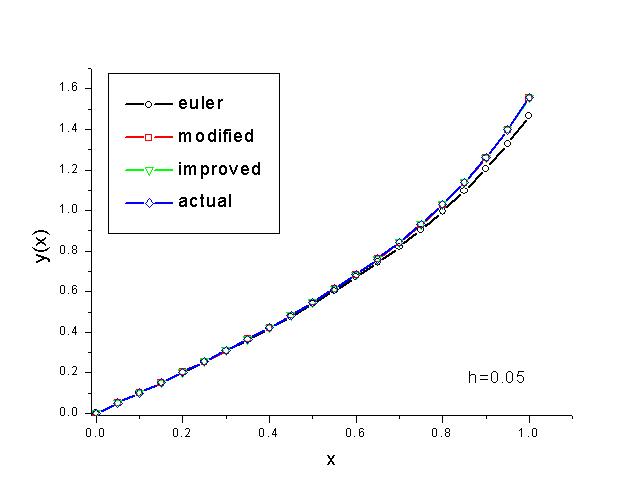
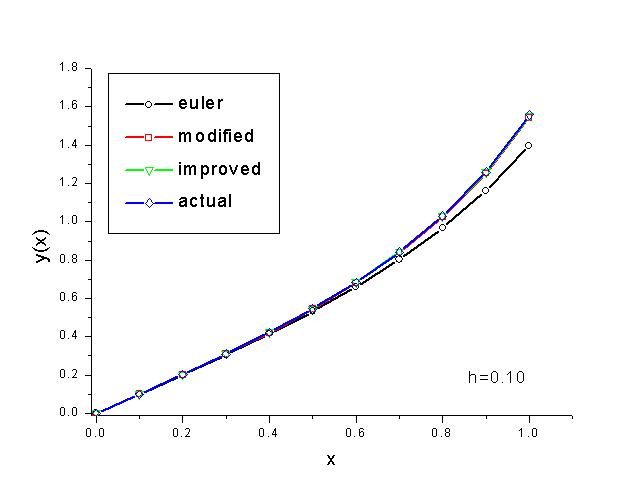
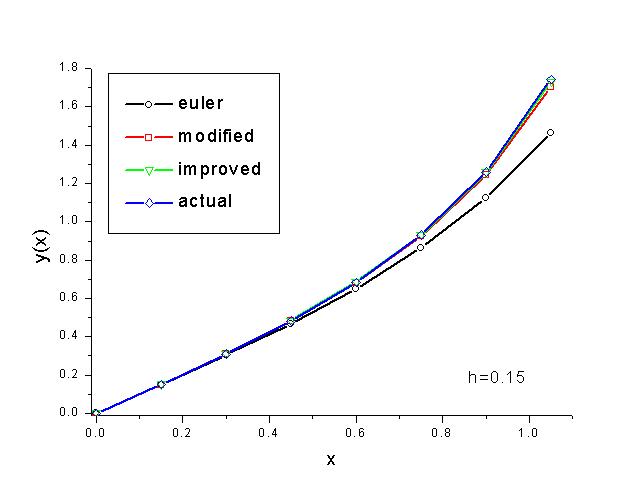
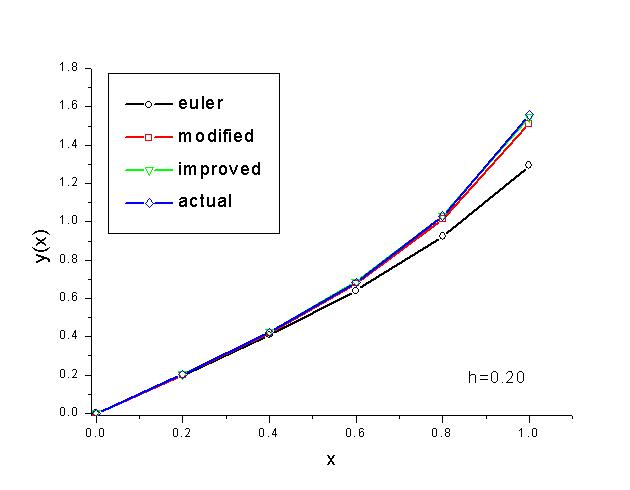
The C implementation for this problem is given here. Although the basic Euler method forms the conceptual foundation for almost all ODE solvers, it is notoriously known to be unstable meaning that the numerical solution will quickly diverge from the true solution unless the step size is chosen to be sufficiently small. This can be seen from the last graph in the following set of graphs. While with h=0.05, all three solutions follow the exact solution closely, the regular Euler solution diverges from the exact solution quickly when h=0.2.
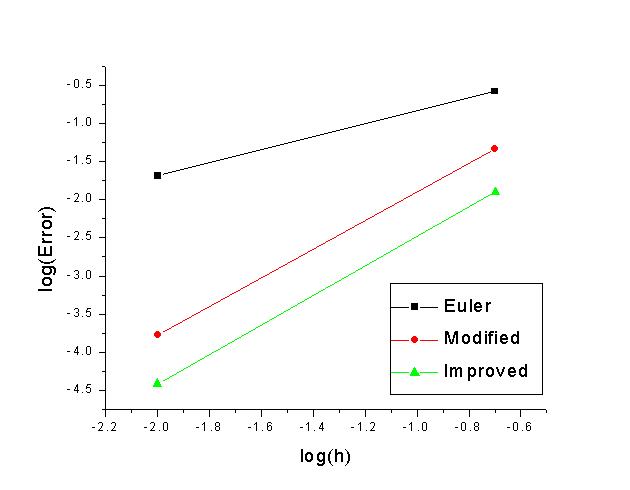
On the other hand, both the modified and improve Euler methods provide much more accurate results. This is due to their better stability characteristics and their smaller expected one step error. While the regular Euler one step error is on the order of h2, the other two methods' one step errors are on the order of h3. In the following graph, the log of the accumulated error is plotted against the log of the step size. The slopes in this graph give rough estimates on these growth rates. (Note: Since the accumulated error is used instead of the one-step error, the growth rate is roughly one less than the values quoted above, i.e., O(h) for regular Euler and O(h2) for the other two methods.)
The bottom line is that with these simplier ODE solvers, in order to have accurate and stable results, small step sizes must be used.The exact solution for this ODE is y=tan(x).