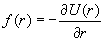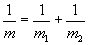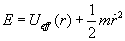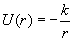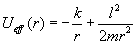PHYS 510 - Computational Physics I

Assignment 2: Functions and Roots

Spring 2010

Date Assigned: Jan. 26, 2010
Date Due: Feb.2, 2010

Reading Assignment

  1. Chapter 9: Root Finding in Press

Assignment 2

The assignment is to design and write algorithms for the the following problems. You may choose to use either a NT or a LINUX platform for this assignment. The code may be developed in either C/C++, Fortran, Java, or Matlab.
  1. The Two-Body Central Force Problem
    We would like to consider the motion of two bodies moving under the influence of a mutual central force. [Note: a central force is a force that acted only along the axis joining the two bodies.] In particular, consider two point masses m1 and m2, where the only forces are those due to an interaction potential U. We further assume that the interaction potential U is resulted from a conservative central force f(r) where

    and r is the scalar distance between the two masses. With this simplications, this original two bodies problem reduce to an equivalent one-body problem with a reduced mass m given by

    moving in a plane about a fixed center of force. In polar coordinates, the motion of the reduced mass is then given by the simple equation,
    .
    l on the right hand side of the equation is the constant angular momentum of the system. One can treat the combination of this angular momentum term together with f(r) as a combined effective force f'(r) for the reduced mass. Equivalently, one can consider this as a one dimensional problem for a particle m moving in an effective potential energy Ueff(r) given by
    .
    From the conservation of energy, the motion of the reduced mass can equivalently be described by the following equation,

    where E is the total energy of the system. Note that the right hand side is simply the sum of the effective potential energy term (first) and a kinetic energy term (second). For this one dimensional problem, one can easily classify the types of possible motions by considering a graph of this effective potential Ueff(r) as a function of r. As an example, consider the familiar case where U(r) is from the attractive inverse square force law, i.e.
    .
    k is a positive constant. (Note: k = Gm1m2 for the Newtonian gravitational force.) The potential energy for this force is

    and the corresponding effective potential energy is

    A picture of this effective potential is shown below with the two colored lines representing its two components.

    Since the kinetic energy must be positive for all possible motions, there are three basic types in this case. For E=E1, E will be larger than Ueff(r) for all r except for small r values (r < rturning point)so that the sysetm's kinetic energy will be positive for all r except for small r values. This corresponds to unbounded motions such that the two masses come toward each other from infinity. After they have reached their closest turning point, they will move away from each other again. For E=E2, the kinetic energy will be positive only in a limited range of r values between rmin and rmax. In this case, the two masses will be bounded together with a maximum distance rmax and a minimum distance rmin. Lastly, if E=E3 (at the minimum of the effective potential Ueff(r)), the system will be restricted to move in circular motion at a fixed radius r0. For forces given by the inverse square law or the Hook's law, analytic solutions for these r values can be calculated. However, for an arbitrary type of force, these must be numerically obtained.

    For this problem, we assume the following form for the interaction potential U(r)
    .
    Take l2/2m=0.01, k=1.0, a=0.2 and do the following:

    • Plot U(r), l2/(2mr2), and Ueff(r) as a function of r.
    • For positive energies, the motion of the system will correspond to the unbounded states. Take E=10, numerically calculate the turning point radius rturning point. (Hint: The turning point is located at the r value where the kinetic energy is zero.)
    • For negative energies, we have the bounded states. Take E=-10, numerically calculate the minimum rmin and the maximum rmax radius of the orbit. (Hint: Again, these extreme values occur at where the kinetic energy is zero.)
    • At the minimum of the effective potential Ueff(r), the two body will be in circular motion. Find the radius r0 of this circular orbit. What is the total energy E of the system at this point?

    Numerical Notes:

    Since a root-finding algorithm is one of the simplest numerical algorithms, you should write your own implementation for it. For this problem, you are not allowed to directly use pre-existing routines from NR or any other sources. However, you are welcome to use them as references.

    As we have mentioned in class, if one is given a valid bracket, the bisection method will always work but its convergence might be slow. On the other hand, if a good initial guess is given, the Newton's method converges quadratically faster. Your implementation of the root-finding code should include both methods. In particular, a default bisection part should be used for initial rough estimations and for situations when the Newton's method does not return estimates within the bracket. Then, a Newton's method part should be used to "polish" a rough estimate to the required precision. For this problem, you are required to report your answers to within single precisions of your machine.

    Solution

    For the parameters chosen, the effective potential Ueff(r) has a minimum and one should expect bounded states for a given energy range. A graph of U(r), l2/(2mr2), and Ueff(r) is plotted as a function of r below.

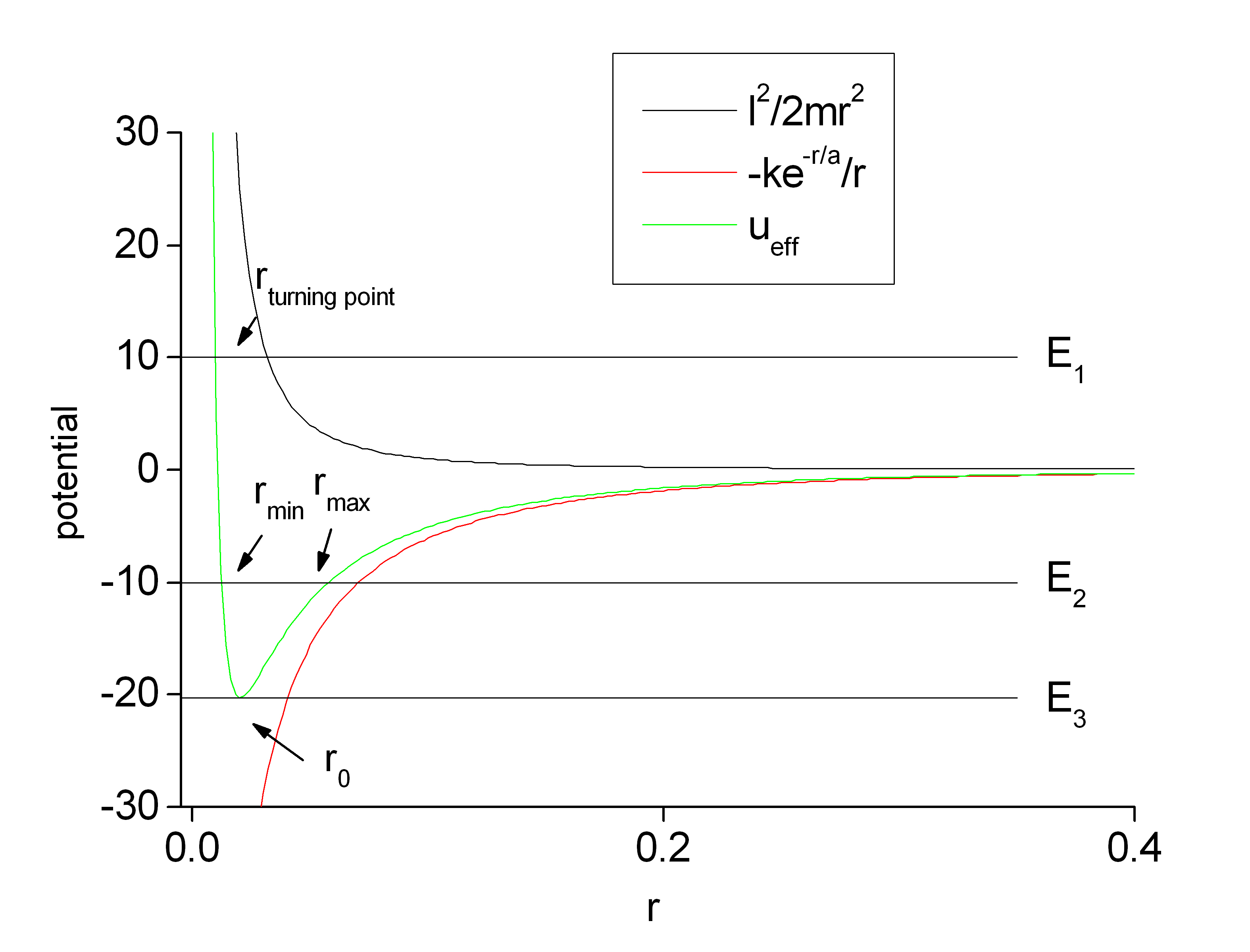
    For positive energies, the motion of the system will correspond to the unbounded states. For a given positive energy, the two bodies starting from infinity will initially come toward each other until they reach the turning point rturning point. At the turning point, E=Ueff(rturning point) and its kinetic energy is zero. To find this turning point, we need to look for the zero of the function E-Ueff(r). From the graph of Ueff(r), we can see that E-Ueff(r) will be a monotonic increasing function upto the r0 and rturning point is located somewhere between ~0 and r0. From a rough graphical estimate, I have chosen [0.005,0.02] as the initial bracket for our zero-finding routine. [Note: Since Ueff(r) blows up at r=0, one should choose the left bracket close to but not too close to 0.] As we have discussed in class, our general zero-finding routine will first use the mid-point of the bracket as the initial guess for the Newton's step. Then, if the Newton's estimate is within the bracket, it will be accepted. If it is outside the bracket, a bisection step will be taken instead. A C implementation of this algorithm is given here. A sample output from this program is here. With E=10, rturning point is found to be at 0.00953477515682641. For a prescribed relative tolerance of 10-12, it took 7 Newton's steps to reach the desired answer.

    With negative energies, the orbits will be bounded. There will be two turning points correspond to rmin and rmax. Again, from a rough graphic estimate, we have chosen the following values [0.005,0.02] and [0.02,0.1] for the two brackets. We used the same program as before and the outputs in this case are given here. With E=-10, rmin and rmax are found to be at 0.0122162023178549 and 0.0576140173757341 respectively. The program took respectively 8 and 5 Newton's steps to achive the 10-12 tolerance level.

    The last part of the assignment asks for the location of the minimum of Ueff(r) where the orbit is expected to be circular. Since we are interested in the minimum of Ueff(r), we want to find the zero of its derivative dUeff(r)/dr. The basic program is still the same but we need to replace the function call to dUeff/dr instead of Ueff itself. A revised version of the program is given here and a sample output is here. r0 is found to be at 0.0200948852273108. The required energy for the system to be at r0 is equal to Ueff(r0)=-20.2424232108433.

    Summary of result: