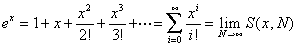Since real numbers are stored in computers with a finite word length, a machine representation of a real number can only be recalled by a computer with limited precision. [Please read section 2.14 in Landau for more detail.] To summarize, one can visualize the effect of machine precision by the following simple mathematical operation: x = 1 + e, where e is a small real number. The machine precision of a computer is defined by the maximum positive e that can be added to 1 such that x is still recongized by the computer as identically 1. The machine precison e is approimately 10-7 for single precision and 10-16 for double precision.
For this problem, you need to write a program to determine the machine precision of your machine (within a factor of 2) for double precision floating-point operations. [Please read section 1.5 in Landau]. The output of your program should contain at least two columns showing the value of x and e as e gets increasing small. What is the value of e for your machine?
Solution
This problem is relatively straight forward. A C implementation of the code is given here. The output from this program is here. There are three columns in this output file: iterations, x value, eps value. One can clearly see from this list of numbers that when e is approimately 1x10-16, x becomes indistinquistable from 1. In particular, eps=1.11x10-16 is the largest such value for this machine implementation. One shoule note that it is not correct to say that computer with double precision cannot handle numbers smaller than 10-16. As discussed in lecture, the problem emerges when one wants to add one large number and one small number together when their ratio is comparable with e. In the computer, the mantissa part of the two numbers can only be added if the smaller number is scaled to have the same exponent as the larger one. However, this shifting of bits in the rescaling process will result in the reduction of significant bits in the mantissa for the smaller number. In the limiting case at the machine precision, all significant bits in the smaller number will be lost in the operation.
Problems with subtractive cancellations can occur in the blind application of one of the most basic mathematical equations, the quadratic formula. The standard quadratic equation,
ax2+bx+c=0
has the standard solution
(1).
However, in the case when b2 is much larger than 4ac, subtractive cancellation can occur in the numerator resulting in potential loss of significant figures. A remedy is to use an alternative expression for the quadratic formula when substractive cancellation is suspected. This alternative quadratic formula is given by
(2).
By a simple inspection, one can see that subtractive cancellation might occur in x1 and y2 if b>0 and it might occur in y1 and x2 if b<0. [Please read section 3.4 in Landau for more details.]Please do the following for this problem:
- Write a program that calcuate the four solutions x1, x2, y1, and y2 for the quadratic equation with a set of arbitrary values of a, b, and c.
- Take a=b=1, and c=10-n, n=1,2,3,... and compute the four solutions for increasing n. Please make sure that your output data have enough significant figures.
- What is the largest n when machine precision causes Eq. (2) to fail?
- Since b>0, subtractive cancellation will NOT occur in y1 and x2. Treat these two values as the accurate solutions to the quadratic equation and calcuate the errors in the other two solutions x1 and y2. Plot the fractional relative errors of x1 and y2 as a function of 4ac in a log-log graph.
- Comment on your results in relation to the machine precision.
Solution
A C implementation for this problem is given here and a listing of the four solutions is here.
As one can see from this data file, when 4ac/b2 is less than machine precision (roughly 10-16), the expression b2-4ac is treated by the computer as literally b2. Since the denominator in Eq. (2) will then be simply b-sqrt(b2), the numerically computed value from this equation will return infinity (last few values in the fourth column). For this problem, 4ac/b2 reaches machine precision when n = 17.
However, significant loss of precision due to subtractive cancellation begins to occur long before this obvious numerical failure. The following is a log-log plot of the relative errors in the "bad" solutions resulted from subtractive cancellation.
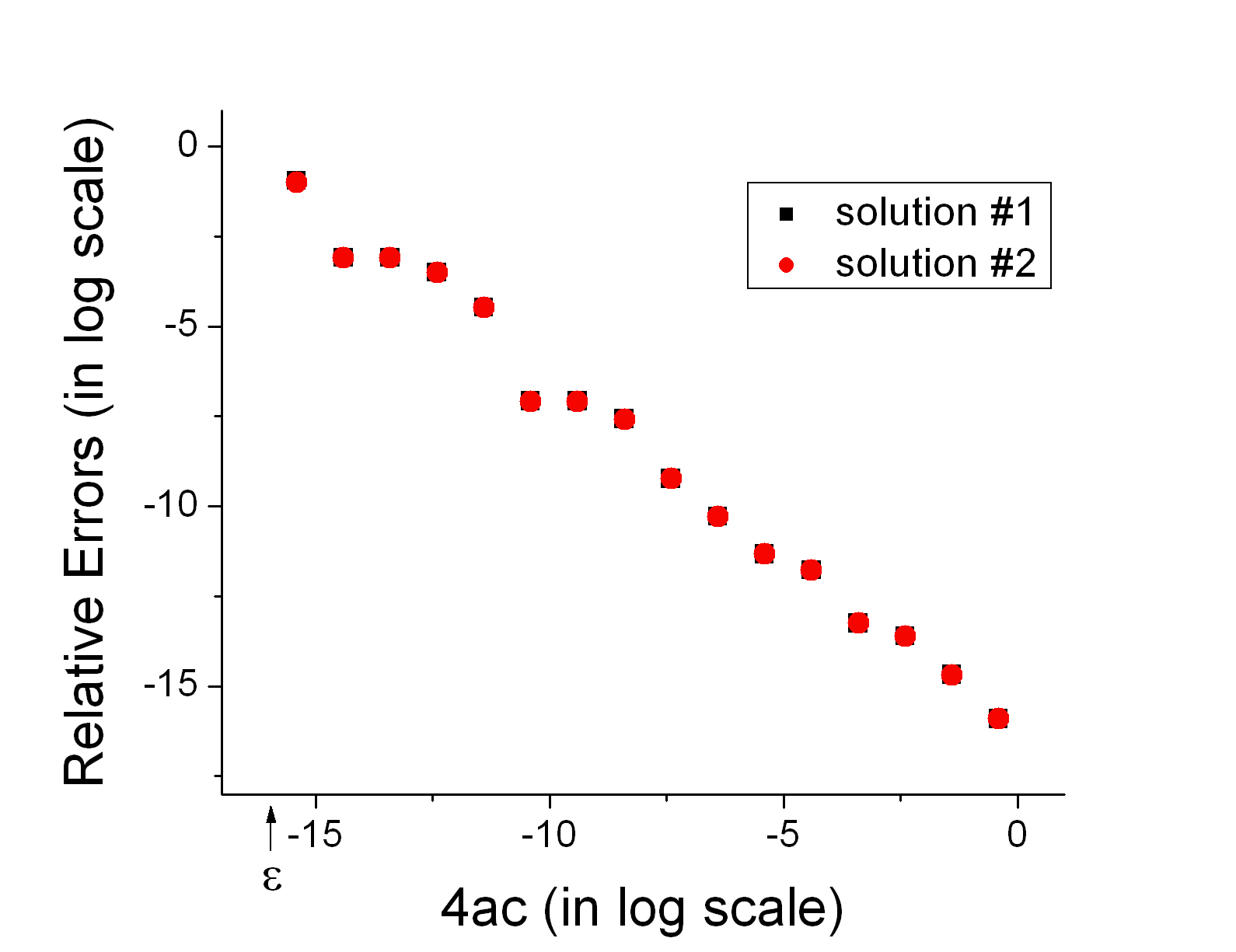
One can clearly see the exponential rise of the relative errors in the "bad" solutions from this graph as the ratio 4ac/b2 [recall b=1] gets closer to machine precision. One should note that this loss of precision and the catastrophic failure of Eq. (2) due to the exact cancellation of its denominator is purely a numerical problem. Mathematically, there is nothing wrong with either Eq. (1) or (2). They are both valid solutions to the quadratic equation. The numerical problem that we observed in this example came from the finite precision of the computer and it was dramatically magnified by a "bad" numerical pitfall, namely, subtractive cancellation. However, subtractive cancellation is only one of the many possible numerical pitfalls. The study of numerical analysis is to learn to avoid these pitfalls and to minimize numerical errors.
SolutionConsider the Taylor expansion for the exponential
where S(x,N) is the partial sum with N+1 terms.
- Write a program that plots the partial sum S(x,N) and its absolute fractional error, |S(x,N)-ex|/ex, versus N (up to N=30) for a given value of x. Test your program for x=10,2,-2, and -10. From the plots, explain why this is not a good way to evaluate ex when x<0. [Note: when x<0, the Taylor's expansion of the exponential is an alternating series.]
- Modify your program so that it uses the identity ex=1/e-x~1/S(-x,N) to evaluate the exponential when x is negative. Explain why this approach works better.
The partial sum and its absolute fractional error is plotted in the following two graphs for the four different x values.
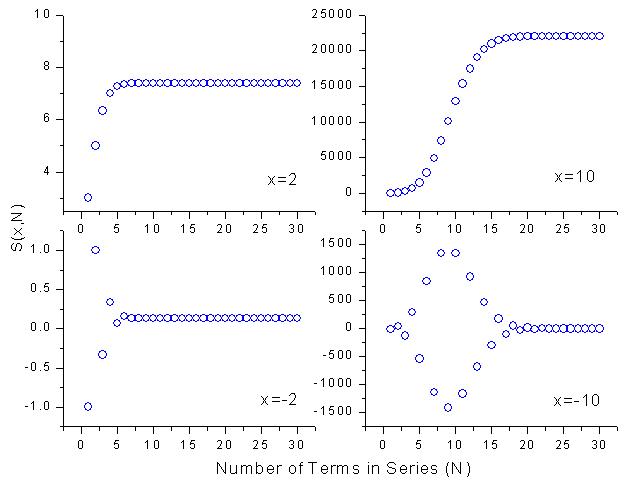
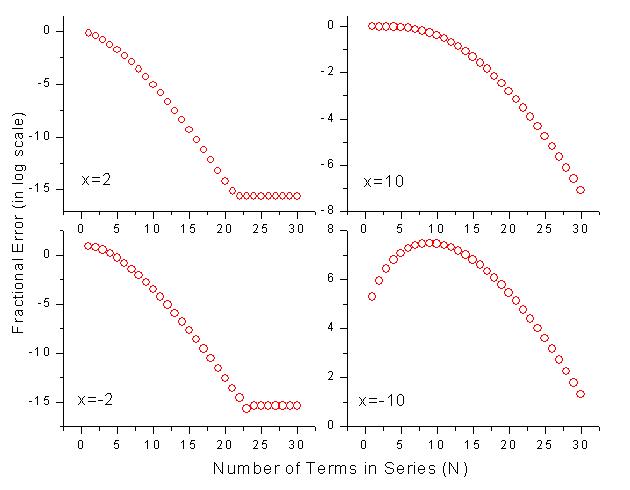
One obvious problem with the partial sum for negative x is the alternating values. This is due to the fact that the partial sum in the Taylor expansion for the exponential is an alternating series for x<0. For x ~0 [x=-2], this alternating feature is not really a big problem, the series goes up and down for a few N. It then quickly converges to its asympotic value. On the other hand, for x equal to large negative value [x=-10], this becomes a very bad idea to calculate the exponential function. The partial sum alternates between extremely large values even for N up to 15. As one can see from the absolute fractional error graph, the fractional errors are order of magnitues larger than the expected value for e-10. Although the series will evenly converge close to the expected value for e-10, the subtraction of large numbers to get small number will amplify roundoff errors. The final lost of significant figures will be large.
One easy way to use the Taylor expansion to evaluate the exponential without the problem of the alternating series for x<0 is to calculate ex=1/e-x~1/S(-x,N) for x<0. The following are the absolute fractional errors calculated for x=-2, and -10 using this method.
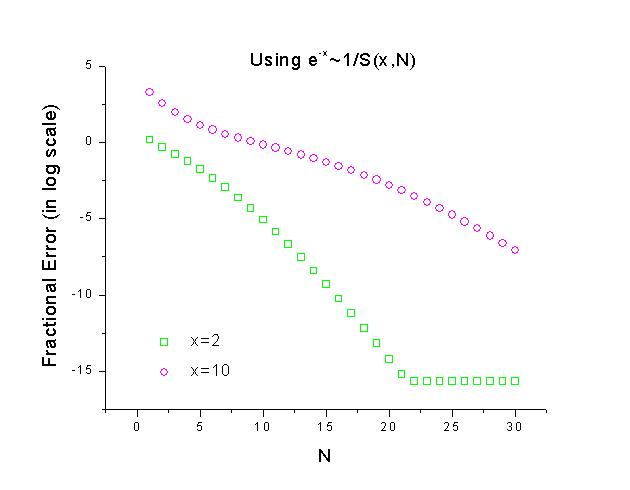
As one can see from this graph, the partial sums do not alternate and begin to converge to the expected values right away.
A list of the program in C can be found here.